日期: 2020 年 8 月 25 日

我们紧接着前一篇的QuickFind继续探讨，因为QuickFind采用连通状态设置值相等的算法，每一次操作都需要遍历整个数据表，并可能有大量的赋值操作，有没有一种稍微优化的算法，这就是这篇需要研究的QuickUnion

QuickUnion 不再将数组的各个节点看作平级，而是构造一种树状结构。其核心思想是

1.将父节点的索引值填充到当前节点中，而不是用节点本身的值去覆盖

2.构造的数组元素在不存在父子关系的时候，索引值等于节点值，比如第0号元素等于0，第2号元素等于2（数组索引从0开始）

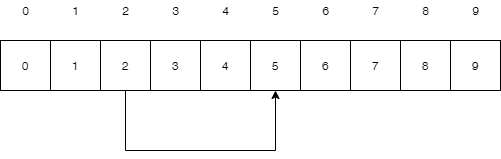
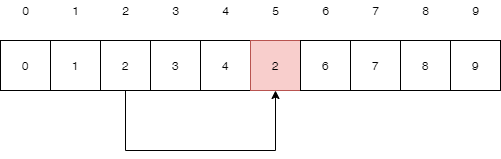
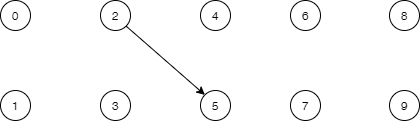
当我们进行第一次union操作时，比如要第3号元素和第4号元素进行合并，将3号元素挂载在4号元素下面，我们把4号元素的索引值4写入第3号元素，表示第3号元素的父节点的位置在第4个位置上，整个数组结构变成如下

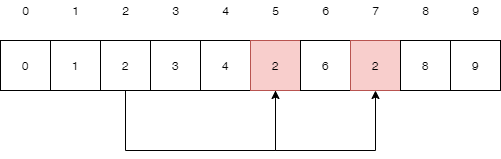
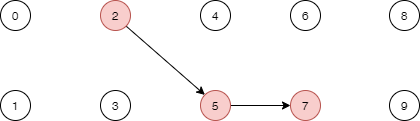
这样，当我们查看到第3号元素的时候，发现他的值不是3，说明这个节点不再是根节点，而变成了一个子节点，那么他的父节点在哪呢，就是他的值所指向的位置，第4个元素，如果是7，那他的父节点就是第7位置的节点，依此类推。如果他的父节点还不是根节点，继续往上找，直到找到本身的索引值等于其存储的值的那个位置，即为根节点。于是，我们可以写一个函数来查找根结点

/**
   * 查找根节点
   * @param p 待查找的节点索引
   * @return 根节点索引
   */
  def root(p:Int): Int = {
      var root = p
      while (root != arr(root)){
        root = arr(root)
      }
      root
  }

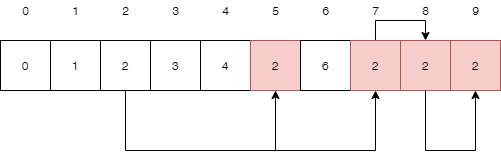
当我们要连通两个节点的时候，不再直接操作这两个节点，而是先查找到这两个节点的根节点，然后在两个根节点之间进行 union 操作。我们合并一些节点得到如下结构

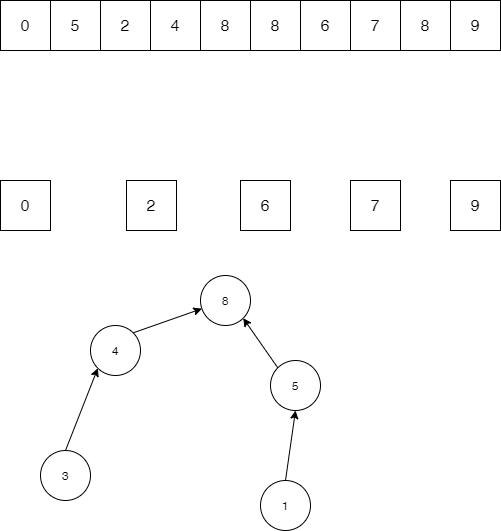
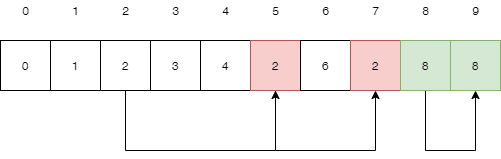
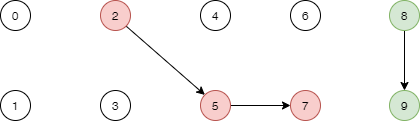
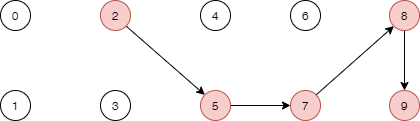
还剩0 2 6 7 8 为独立节点，1 3 4 5 8 已经构成一个树形结构，他们的根节点为8。于是我们判断两个节点是否连通，只要查看他们的根节点是否一致即可，用函数实现如下

/**
   * 查看两个节点是否连通
   * 连通 true 否则 false
   * @param p 待查询的p节点索引
   * @param q 待查询的q节点索引
   */
  def connect(p:Int,q:Int): Boolean ={
    if(root(p) == root(q)) true else false
  }

而union操作的逻辑也很简单，先查找到两个节点的两个根节点，如果两个根节点不一致则我们定义连接者根结点为子节点，待连接者根结点为父节点。只要将父节点的索引值覆写子节点的值即可。如果两个根节点一致，则表示两节点已是连通状态，不进行操作

/**
   * 连通两个节点
   * @param p 连接者节点
   * @param q 待连接者节点
   */
  def union(p:Int,q:Int): Unit ={
    val root_p = root(p)
    val root_q = root(q)
    if(root_p != root_q){
      arr(root_p) = root_q
    }
  }

最后完整代码如下，在scala2.12.10下测试通过

package com.datacrafts.digitalevers.algorithm

class quickUnion {

    val arr:Array[Int] = new Array[Int](10)
    for(i <- 0 to 9){
      arr(i) = i
    }

  /**
   * 查找根节点
   * @param p 待查找的节点索引
   * @return 根节点索引
   */
  def root(p:Int): Int = {
      var root = p
      while (root != arr(root)){
        root = arr(root)
      }
      root
  }

  /**
   * 查看两个节点是否连通
   * 连通 true 否则false
   * @param p 待查询的p节点索引
   * @param q 待查询的q节点索引
   */
  def connect(p:Int,q:Int): Boolean ={
    if(root(p) == root(q)) true else false
  }

  /**
   * 连通两个节点
   * @param p 连接者节点
   * @param q 待连接者节点
   */
  def union(p:Int,q:Int): Unit ={
    val root_p = root(p)
    val root_q = root(q)
    if(root_p != root_q){
      arr(root_p) = root_q
    }
  }
}

object quickUnionDemo{
  def main(args: Array[String]): Unit = {
    val qu = new quickUnion
    qu.union(3,4)
    qu.union(4,8)
    qu.union(1,5)
    qu.union(5,8)
    for (elem <- qu.arr) {
      print(elem)
    }                       //0524886789
    println()
    println(qu.connect(0,3))  //false
    println(qu.connect(1,3))  //true
  }
}

考虑到树的最大深度，无论是union还是connect都会进行两次遍历root节点操作，依旧是一个N^2的时间复杂度的算法，无法进行大规模化运算

需要得知两个物件是否已经被连接起来是现实生活中经常遇到的问题，比如复杂电路板上的两个原件是否是连通的，再引申一下，迷宫的两个出口是否可以形成一条路径，也可以归属此问题。下面将使用一维数组来简化解释该算法

有0-9个数在一维数组的0-9个位置上依次排列，现在要将第2位和第5位进行连接，我们称第2位为连接者，第5位为被连接者，同时我们定义，

当连接者和被连接者都是一个独立节点（即在数组中还没有重复的值存在），使用连接者去覆盖被连接者

可见，第5位也被改写成了数字2，于是第2位和第5位连通了起来。然后继续这一过程，将第5位再和第7位连接起来

继续连通第8位和第9位

再继续连通第7位和第8位

这样，当我们需要判定两点是否连通的时候，只需判断两者的值是否相等就可以了。下面将采用Scala来实现这一算法

package com.datacrafts.digitalevers.algorithm

class connectClass {

  val arr:Array[Int] = new Array[Int](10)
  for(i <- 0 to 9){
    arr(i) = i
  }

  /**
   * 连通两个节点
   * @param p  连接者为止
   * @param q  被连接者位置
   */
  def connect(p:Int,q:Int): Unit ={
     for(i <- 0 until  arr.length){
       if(arr(i) == arr(q)){
         arr(i) = arr(p)
       }
     }
  }

  /**
   * 测试两点是否连通
   * 连通为 true 否则为 false
   * @param p
   * @param q
   */
  def isconnect(p:Int,q:Int): Boolean ={
    if(arr(p) == arr(q)) true else false
  }
}

object connectClass{
  def main(args: Array[String]): Unit = {
    val cc = new connectClass
    cc.connect(1,3)
    cc.connect(3,5)
    println(cc.isconnect(1,5))
    println(cc.isconnect(1,6))
  }
}