连通算法-Scala实现《算法》第一章(QuickUnion)改良版

接上一篇的QuickUnion算法，篇末曾提及该算法不适合大规模化的运算场景，因为在某些情况下会构造一棵很深的树，比如下面这种情况:

    val qu = new quickUnion
    qu.union(0,1)
    qu.union(1,2)
    qu.union(2,3)
    qu.union(3,4)
    qu.union(4,5)
    qu.union(5,6)
    qu.union(6,7)
    qu.union(7,8)
    for (elem <- qu.arr) {
      print(elem)
    }

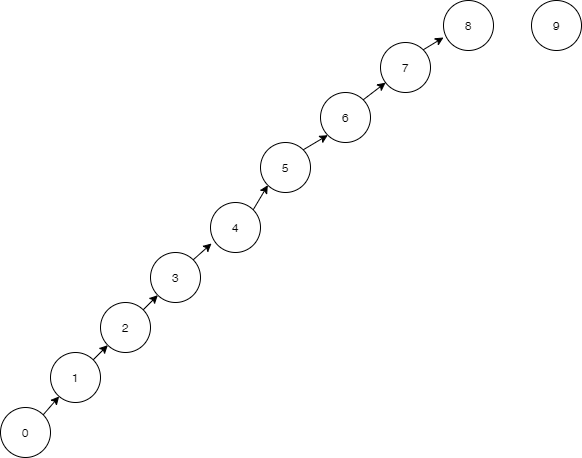
如果要比较 0和9两个节点的连通性

qu.connect(0,9)

需要遍历了整棵树，从节点0一直检索到节点8，之所以会造成这种局面，主要是因为我们默认 union 函数的第一个参数的根节点作为子节点，第二个参数的根节点作为父节点，如果左边参数是一颗更深的树，右边参数是一棵小树。这样相当于是将一棵大树挂载到一棵小树上，使得深度不断加大，同时也不断加大算法的时间度。

对此我们的优化建议是，不再强制左右参数谁是父节点，谁作为子节点，而是依据两者树的深度，确保一直是把小树挂载到大树下，从而最大限度限制树深度的递增。于是我们额外维护一个数组 arrTreeLevel ，里面存放每个根节点的树的深度，如果该节点已经作为子节点挂载到其他节点下，则置为0。

如果两棵树的深度一致，则自增1，如果一方大，另一方小，则小的作为子节点，大的作为根节点，深度保持不变。所以只要对 union 函数稍作修改即可，其他程序不需要改动，全部代码如下:

package com.datacrafts.digitalevers.algorithm

class quickUnion {

    val  arrTreeLevel:Array[Int] = new Array[Int](10)

    val arr:Array[Int] = new Array[Int](10)
    for(i <- 0 to 9){
      arr(i) = i
      arrTreeLevel(i) = 1
    }

  /**
   * 查找根节点
   * @param p 待查找的节点索引
   * @return 根节点索引
   */
  def root(p:Int): Int = {
      var root = p
      while (root != arr(root)){
        root = arr(root)
      }
      root
  }

  /**
   * 查看两个节点是否连通
   * 连通 true 否则false
   * @param p 待查询的p节点索引
   * @param q 待查询的q节点索引
   */
  def connect(p:Int,q:Int): Boolean ={
    if(root(p) == root(q)) true else false
  }

  /**
   * 连通两个节点
   * @param p 连接者节点
   * @param q 待连接者节点
   */
  def union(p:Int,q:Int): Unit ={
    val root_p = root(p)
    val root_q = root(q)
    if(root_p != root_q){
      if(arrTreeLevel(root_q) >= arrTreeLevel(root_p)) {
        arr(root_p) = root_q
        if(arrTreeLevel(root_q) == arrTreeLevel(root_p)){
          arrTreeLevel(root_q) += 1
        }
        arrTreeLevel(root_p) = 0
      } else {
        arr(root_q) = root_p
        arrTreeLevel(root_q) = 0
      }
    }
  }
}

object quickUnionDemo{
  def main(args: Array[String]): Unit = {
    val qu = new quickUnion
    qu.union(0,1)
    qu.union(1,2)
    qu.union(2,3)
    qu.union(3,4)
    qu.union(4,5)
    qu.union(5,6)
    qu.union(6,7)
    qu.union(7,8)
    for (elem <- qu.arr) {
      print(elem)
    }                       //0524886789
    println()
    println(qu.connect(0,9))  //false
  }
}

附:《算法》一书中是采取比较树节点数量大小的方式来决定谁是子节点，谁是根节点，然后再“压平”来减少树的深度。笔者认为，直接跟踪树的深度更加直观，读者可自行判断